A class of data analysis procedures for statistical hypothesis testing that, unlike parametric statistical analysis, makes no assumptions about the sampling distribution of a statistic being evaluated, nonparametric statistical analysis is also called distribution-free statistical analysis. The two terms have a slightly different meaning but are frequently used interchangeably. While nonparametric statistical inference is not bound to a priori specified parameters of a statistical model, distribution-free statistical inference is not bound to an a priori specified sampling distribution of a statistic that serves as estimation for a parameter in a population.
Nonparametric Or Parametric Statistical Analysis?
Two indications suggest preferring a nonparametric over a parametric statistical analysis: (1) measurement problems and (2) problems with the assumptions of a parametric statistical test.
Measurement problems: in a strict sense, the results of a parametric statistical analysis cannot be meaningfully interpreted if the data were measured on a measurement level other than an interval or ratio level. While most statisticians and researchers agree on the fact that ordinal data require a nonparametric approach, there is still disagreement over whether statistical tests for analyzing nominal data require a parametric or nonparametric statistical analysis. Given large samples, the common practice is to analyze nominal data in a parametric fashion by referring to a chi-square sampling distribution. However, operating with small samples requires analyzing nominal data with a nonparametric approach (see example below) since a specific sampling distribution with known parameters is missing. For the same reason, nonparametric statistical tests are commonly labeled as statistical tests for the analysis of small samples.
Problems with the assumptions of a parametric statistical test: parametric statistical tests are bound to mathematical-statistical assumptions such as homogeneous variances in populations or normally distributed variables. If the collected data suggest that mathematical-statistical assumptions are violated, the results of a parametric statistical analysis may be biased. Many parametric statistical analyses are either robust or conservative test procedures. This means that results are either unbiased or favor the null hypothesis in a statistical test decision even if assumptions are violated. Communication (empirical) researchers usually consider this a minor problem. However, conservative parametric test decisions typically are associated with a reduced power of the corresponding statistical test. In other words, it is more difficult to detect a statistically significant result with a parametric statistical test analysis if the mathematical-statistical assumptions are violated. It can be shown that under the condition of violated assumptions a nonparametric test analysis may result in an unbiased test decision with higher power than its parametric equivalent.
In summary, a nonparametric test analysis is recommended if data have been collected on an ordinal or nominal level, if sample sizes are small, and if there is evidence that mathematical-statistical assumptions of a parametric test analysis have been violated.
A Selection Of Nonparametric Statistical Analyses
Communication researchers can select among numerous nonparametric statistical procedures for analyzing data. Typically, a useful categorization of nonparametric procedures refers to measurement level and the number of variables as categorization criteria. The following (limited) selection of nonparametric statistical analyses covers just a few of the most common nonparametric test procedures.
Nominal data, one variable: the binomial test analyzes the statistical significance of deviations from a theoretically expected distribution of dichotomous observations (such as the flip of a coin). The multinomial test generalizes the binomial test for observations with more than two categories.
Nominal data, two variables: the Fisher-Yates test (see example below), which is also called Fisher’s exact test, examines the significance of an association between two variables with two categories each (which defines a 2 × 2 contingency table). The two versions of the Fisher-Freeman-Halton test generalize the Fisher-Yates test concept for k × 2 (two variables, k categories of the one and 2 categories of the other variable) and k × m (two variables, k categories of the one and m categories of the other variable) contingency tables.
Ordinal data, one variable: the median test and the Mann-Whitney-Wilcoxon test (also called Wilcoxon rank-sum test) analyze whether the difference in medians between two independent samples is statistically significant. The Kruskal-Wallis test can be applied for more than two independent samples (as in a one-way analysis of variance). Similar to a repeated measures analysis of variance, a Friedman test can be applied to analyze differences in dependent samples. Both the Kruskal-Wallis test and the Friedman test require a transformation of measurements into ranks. There are nonparametric statistical test analyses for more than one variable and more than two independent samples. These procedures, however, are rather complex and require a profound mathematical-statistical background to understand.
Interval data: unlike the aforementioned statistical tests, nonparametric statistical tests for interval data do not require a prior transformation of measurements into ranks, which usually results in a loss of information. These test procedures are indicated if the size of samples is small and, therefore, parametric analytical procedures are out of the question. The Fisher-Pitman Randomization test, for example, analyzes whether differences between two independent samples are statistically significant (or in other words, whether two samples originate from the same population). The Fisher Randomization test analyzes the same hypothesis for two dependent samples.
In addition to nonparametric procedures for testing differences in two or more samples, numerous nonparametric correlation coefficients for the analysis of associations between ordinal variables are available. The most common nonparametric correlations are the Spearman’s Rank Correlation (ρ) and Kendall’s Rank Correlation (τ) for ordinal data.
Example
The nonparametric Fisher-Yates test and the corresponding parametric chi-square test for 2 × 2 contingency tables will be used as an illustration of the nonparametric test concept.
A media researcher is interested in analyzing whether men tend to prefer nonfiction TV programs, such as documentaries or news, and women tend to prefer fiction TV programs, such as movies. Hence, the specific (one-sided) research hypothesis (H1) under evaluation is: “There is an association between gender and preference (in the population). The preference for TV programs is specific. Men prefer nonfiction TV programs while women favor fiction programs.” The null hypothesis (H0) is: “There is no such association in the specified direction; the variables gender and preference (fiction vs. nonfiction) are independent (in the population).” In mathematical terminology, the research hypothesis can be written as H1: π(men/nonfiction) > π(women/nonfiction), and the null hypothesis as H0: π(men/nonfiction) ≤ π(women/nonfiction).
In a first study a sample size of just n = 15 men and women could be realized. The data collection results in the following 2 × 2 contingency table:
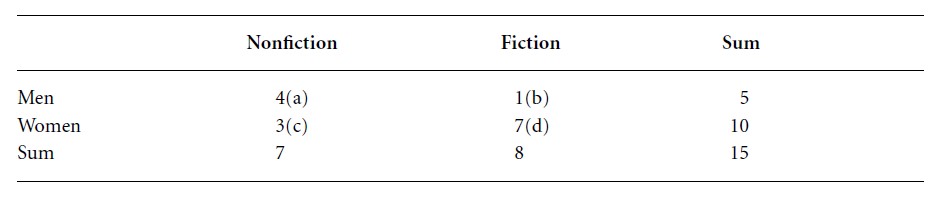
Table 1
The sample data seem to indicate an association in the right direction: men tend to favor nonfiction and women fiction TV programs. The question, however, is whether this association is statistically significant, i.e., is not a random result. As a significance level we choose α = 0.05. Due to the small sample size the nonparametric Fisher-Yates test will be applied. For the first step, we will determine the random probability of the 2 × 2 frequency distribution above. For this we use the hypergeometric probability function according to the following formula:
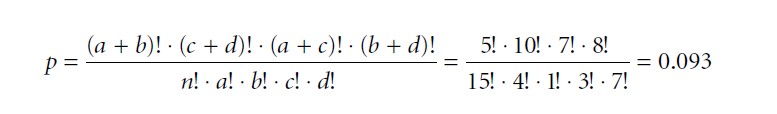
Formula 1
Given the observed marginal sums, the probability that the 2 × 2 table above occurs at random is 0.093 or 9.3 percent. This, however, is just the probability of the observed frequency distribution. In a second step we need to determine how many more extreme frequency distributions (more extreme in the direction of H1) are possible given the observed data. For example, here is another 2 × 2 frequency distribution in which we have moved one man from the fiction to the nonfiction category, and one woman from nonfiction to fiction. The marginal sums remain unchanged:

Table 2
Since one cell already has a frequency of 0, it is impossible to find another more extreme 2 × 2 frequency distribution. The probability of this frequency distribution is:

Formula 2
Thus, the probability that the observed frequency distribution or more extreme frequency distributions occur at random (the null hypothesis) equals the sum of both probabilities: p = 0.093 + 0.007 = 0.1. The null hypothesis cannot be rejected since p > α. Men do not prefer nonfiction over fiction TV programs compared with women – the association observed in the sample is not statistically significant.
In a second study, a larger sample of n = 40 could be reached. After data collection the 2 × 2 contingency table looks like the following:
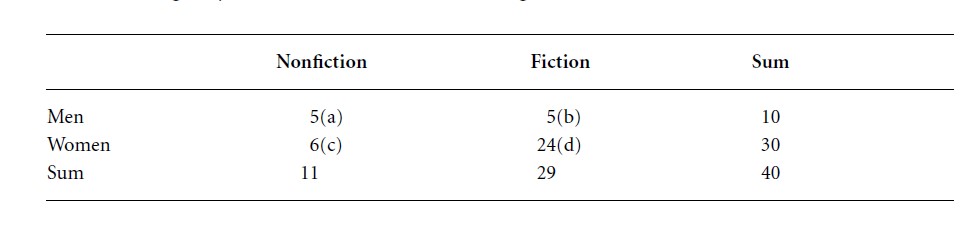
Table 3
Assuming the variables are independent in the population and given the marginal frequency distribution, the expected cell frequencies can be calculated with the following formula:

Formula 3
According to this formula only one of the four cells has an expected frequency of less than 5 (cell a). This result suggests that one has a sufficiently large sample to assume a chisquare distributed sampling distribution of the chi-square test statistics, which is used to evaluate the association between gender and preference in the 2 × 2 table above. Thus, one can use a parametric chi-square test for the analysis of this 2 × 2 contingency table. The empirical chi-square value can be calculated by using the following formula:
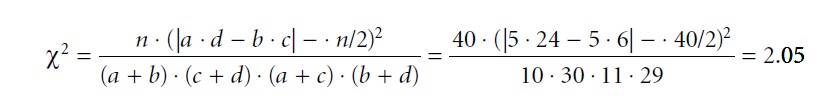
Formula 4
Chi-square values of zero indicate no association between the variables in the sample. Negative chi-square values do not exist. The greater chi-square values are, the less plausible is the null hypothesis. A chi-square value in a 2 × 2 contingency table has one degree of freedom (df = 1), since only one of four cells can be freely modified given fixed marginal sums. Further, the formula provided for calculating an empirical chi-square value refers to a two-sided test (i.e., for testing unspecific hypotheses). To test a specific hypothesis by means of a one-sided chi-square test with one degree of freedom, one can use the relationship between a chi-square distributed and a normal distributed random variable, which is:

Formula 5
Thus, this example would yield a standard normally distributed z-value of z = 1.43, which is the square root of 2.05. The corresponding probability for this and more extreme z-values is, according to the tabulated standard normal distribution, p = 0.076. Again, since p > α we cannot reject the null hypothesis. The parametric test, too, suggests that the observed association between gender and preference in a sample of 40 people is not statistically significant.
References:
- Conover, W. J. (1998). Practical nonparametric statistics, 3rd edn. New York: John Wiley.
- Gibbons, J. D., & Chakraborti, S. (2003). Nonparametric statistical inference, 4th edn. New York: Dekker.
- Higgins, J. J. (2003). Introduction to modern nonparametric statistics. Boston: Duxbury Press.
- Hollander, M., & Wolfe, D. A. (1999). Nonparametric statistical methods, 2nd edn. New York: John Wiley.
- Siegel, S., & Castellan, N. J. (1988). Nonparametric statistics for the behavioral sciences, 2nd edn. Boston: McGraw-Hill.
- Wasserman, L. (2006). All of nonparametric statistics. New York: Springer.
