Information

Common linguistic habits render information as an attribute of messages or data, or as the purpose of human communication – as if information were an objective entity that could be carried from one place to another, purchased, or owned. This conception is seriously misleading. Gregory Bateson (1972, 381) defined information as “any difference which makes a difference in some later event.” Acknowledging that differences do not reside in nature, but are the product of distinctions, leads to the following definition: information is the difference that drawing distinctions in one domain makes in another.

Written messages, for example, vary in very many dimensions – the size and quality of the paper, typefaces, typography, vocabulary use, grammatical constructions, and time of arrival. The number of distinctions that one could possibly draw among these features (and the differences they could possibly make elsewhere) may well be innumerably large. However, psychological, situational, linguistic, and cultural contingencies tend to render only some distinctions meaningful and others irrelevant. This keeps the amount of information that readers actually consider within manageable limits.

Information operates in an empirical domain other than where the distinguishable features reside. Bridging these domains is a matter of abduction, an inference relating data to conclusions. For instance, tree rings inform the forester of the age of a tree. Tree rings become meaningful only when one knows how trees grow rings and informative only when the number of rings correlates with a tree’s age. Abduction is informative; deduction and induction, however, say nothing new.

The paradigm case of conveying information is answering questions. A question implies several answers. Knowledgeable respondents select the most appropriate one among them, which resolves some or all of the uncertainties that prompted the question.

Information “in-forms” – literally – by making a difference within the circularity of cognition and action. Information is not a message effect. It can be sought or ignored. It involves active reading, deciphering, and inferring, which are intentional acts. Receiving something a second time does not add information to the first, but is redundant, save for what had been forgotten. Information may qualify information from previous communications, for example by discrediting its source, revealing overlooked inconsistencies, or rearticulating its context. Information is situationor context-specific. What provides information at one time may be irrelevant at another. What is information for a stockbroker may not be information for an engineer. Talking about one thing excludes talking about something else.

Information is always tied to human agency, to the ability to vary something and make sense of variability. It is absent when one cannot draw distinctions or recognize choices made by others.

Information Theory

No theory can accommodate all intuitive uses of the word “information.” Early measures of information include Harry Nyquist and R. V. L. Hartley’s effort in the 1920s to quantify the capacity of telephone cables, and the statistician Sir Ronald Fisher’s proposal in the 1930s of a measure of information in data. In 1948, Claude E. Shannon published several measures and a widely applicable calculus involving these. To avoid the diverse associations that the word “information” carried, he titled his work “A mathematical theory of communication.” “Information theory” is what others call his theory.

Shannon’s theory, subsequently published with a popular commentary by Warren Weaver (Shannon & Weaver 1949), provided the seed and scientific justification for communication studies to emerge in universities, often consolidating journalism, mass media studies, rhetoric, social psychology, and speech communication into single departments. Shannon’s work was instrumental in ushering in the information society we are witnessing, characterized by digital communication, massive electronic data storage, and computation. Today, information theory is a wide-ranging discipline in applied mathematics.

In his second theorem, Shannon proved that the logarithm is the only function by which two multiplicatively related quantities become additive. This formalizes the intuition that two compact disks (CDs) can store twice as much data as one and that the capacities of separate communication channels or computers can be added.

While the base of a logarithm is arbitrary, Shannon chose the smallest sensible base of 2, log2, as the unit of his calculus. This unit enumerates the number of yes-and-no answers to questions, the number of 0s or 1s needed to store data in a computer, or the number of distinctions or binary choices required to locate something in a finite space of possible locations. Shannon called that unit of enumeration “binary digit” or “bit” for short:

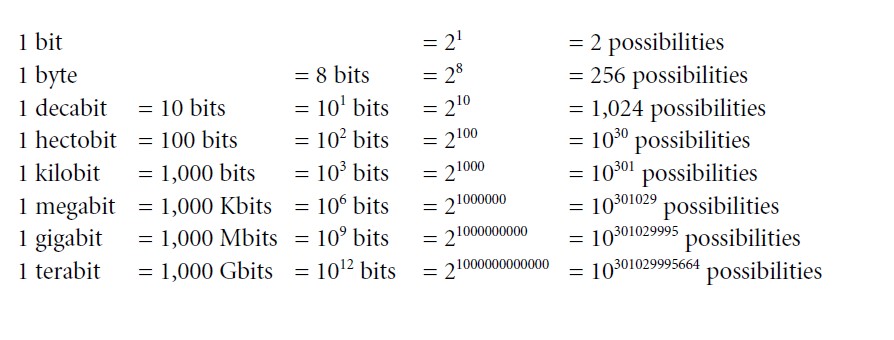
To exemplify, the well-known party game “20 questions” can exhaust 2²⁰ = 1,048,576 or over a million conceptual alternatives. With an array of 20-by-20 light bulbs, one can display 2⁴⁰⁰ or 10¹²⁰ distinct patterns. The human retina has not 400 but about a million independently responsive receptors. Contemporary laptop computers have in the neighborhood of one gigabyte of memory.

The following sketches three concepts of information – logical, statistical, and algorithmic. While Shannon’s original work developed statistical conceptions only, all three acknowledge his second theorem and use bits as units of measurement.

The Logical Theory of Information

This theory (Krippendorff 1967) concerns the logical possibilities of moving on, which depend on the situation S in which one finds oneself. Let U measure the uncertainty one is facing:

Information I, the difference made by drawing distinctions D, can be expressed as the difference between two uncertainties – before a message was received and after drawing distinctions in it:

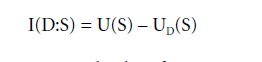
Accordingly, information I is not an entity or thing, but a change in two states of knowing. It measures the difference between two uncertainties of a situation, as Figure 1 suggests. Information is positive when the distinctions drawn in the domain of a message reduce the uncertainty in the situation. It is zero when either no distinction was made, or the distinctions did not make a difference in the domain of interest, be it because the message did not make sense, was already known, or pertained to something irrelevant to the current situation.

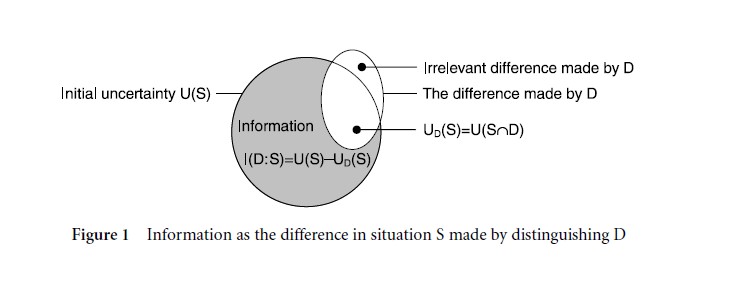
Yehoshua Bar-Hillel (1964) took this to be a semantic theory, as the drawing of distinctions among possible patterns in a message makes a difference in a domain other than the message itself, whether that difference concerns references, connotations, decisions, or actions. For example, the driver of a car who is uncertain about where to turn will be looking for signs that reduce this uncertainty. Typically, drivers face numerous patterns, most of which are irrelevant, perhaps even distracting, and therefore are ignored. Extreme fog prevents making distinctions and information is unobtainable. The latter suggests an important information-theoretical limit to human communication: The information that a message can provide is limited by the number of distinctions one can draw concerning it – the most basic one being the presence or absence of a message. Moreover, both quantities are limited by the uncertainty of the situation, on the one side, and the uncertainty of all identifiable patterns in the message, on the other side:

In human communication, information is largely acquired sequentially, in small, comprehensible doses. For example, each scene in a movie adds something toward its conclusion. For any set of messages, M₁, M₂, . . . M_z, the total amount of information is:

It can be expressed as the sum of sequentially available quantities of information:

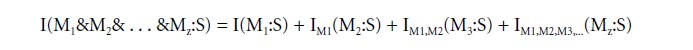
Two messages are logically independent of each other if their separate information quantities add to what they inform jointly:

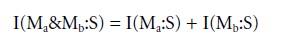
Two messages are redundant to the extent they jointly convey what each would convey separately:

Information can also be expressed in terms of logical probabilities. If N is the number of uncertain possibilities before drawing distinctions D, and N_D after D were drawn:

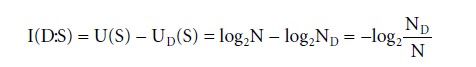
As a function of the logical probability N_D/N, the amount of information is upwardly limited by 1/N.

Shannon’s Statistical Theory of Information

For Shannon, “the fundamental problem of communication is that of reproducing at one point, either exactly or approximately, a message selected at another point” (Shannon & Weaver 1949, 3). While this does not address meaning, reliable reproduction of messages at distant points is a prerequisite for all meaningful use of information and communication technology, whether using letters, telephone, fax, or electronic messaging.

Unlike the logical or semantic theory, Shannon’s theory is a statistical one and concerns itself with averages, with how observed probabilities in one domain relate to observed probabilities in another domain. Shannon called the statistical uncertainty “entropy” and defined it for a particular distribution of probabilities p_a in a variable A by:

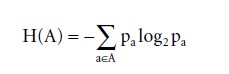
The possibilistic uncertainty U is that special case of the entropy H in which all probabilities p_a are the same, i.e., 1/N_A.

Applied to the simplest case of a channel of communication between just two communicators A and B, Shannon’s basic quantities are the entropies H(A) and H(B) for each variable separately, and the entropy H(A,B) when observing them together:

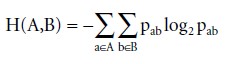
wherein p_ab is the probability of a and b co-occurring, say, in a cross-tabulation of a sender’s and a receiver’s distinctions. From these entropies, the amount of information transmitted between A and B becomes:

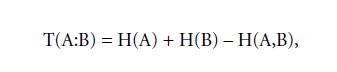
which expresses the degree to which a sender’s choices determine the receiver’s choices.

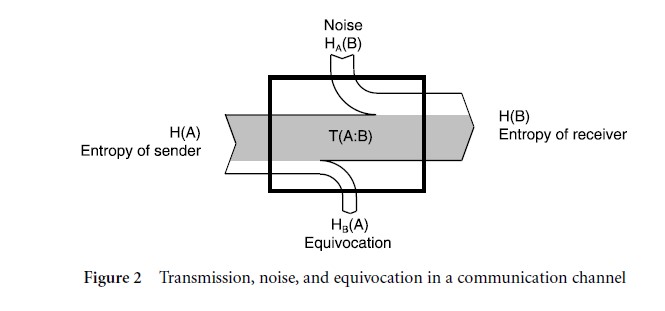
If this amount is zero, then, the sender’s choices do not affect the receiver’s – regardless of the existence of a physical channel between them. When the quantity of transmission equals the entropy of the receiver, then the sender’s choices fully determine what the receiver can see. Otherwise, noise can enter or equivocation can leave a communication channel. Noise provides the receiver with choices that are unrelated to the sender’s choices. The amount of noise is:

which is the entropy that remains in the receiver when the sender’s choices are known. Equivocation, by contrast, is the entropy in the sender when the receiver’s choices are known:

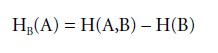
Noise and equivocation relate to transmission by:

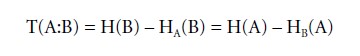
Accordingly, the number of bits transmitted is the entropy in the receiver not due to noise, or the entropy in the sender not lost by equivocation. Figure 2 depicts these entropies.

The capacity C of a channel of communication is:

In serial transmissions from A to Z, noises always add up:

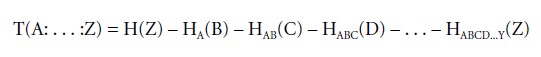
That increase cannot be reversed, as illustrated by repeated copying of documents: copies of copies become worse. Here, Shannon’s theory corresponds with the second law of thermodynamics, according to which entropy always increases over time. In fact, it has been suggested that thermodynamics is a special case of Shannon’s statistical theory of communication.

Shannon’s eleventh theorem addresses the possibility of designing error-correcting codes making use of unused capacities for communication, called redundancy:

Redundancy is evident in repeatedly saying the same thing, avoiding words otherwise available, transmitting images with large continuous areas, and communicating the same message over several channels of communication. In human communication, redundancy protects communication from disturbances; examples are postal addresses with personal names, streets, cities, and states, as opposed to telephone numbers and zip codes, where any one incorrect digit is not correctable. Natural language is said to be 70 percent redundant, allowing the detection of spelling errors, for example.

Shannon’s twenty-first theorem concerns communication in continuous channels. The approach taken is to digitize them. Tolerating an arbitrarily small error makes digitized media less susceptible to noise. This has revolutionized contemporary communication technology.

Kolmogorov’s Algorithmic Theory of Information

Examining the complexity of computation in the 1960s, the Russian statistician Andrei Nikolaevich Kolmogorov (1965) came to conclusions similar to Shannon’s. He equated the descriptive complexity or algorithmic entropy of an object, such as a text or an analysis, with the computational resources needed to specify or reproduce it. Consider the two strings of 0s and 1s:

The first affords a short description in English: “20 repetitions of ‘001,’ ” which consists of 20 characters as opposed to 60, whereas the second affords no simple description. Representing computational objects by strings of 0s and 1s not only conforms to what computers do; it is fortuitous as each amounts to one bit, tying the objects of the theory into the information calculus. So, the length of the sequence s is the log₂ of the number of possible sequences of that length and the –log₂ of its probability. The shortest description of s is called the Kolmogorov complexity K(s), which leads to this inequality:

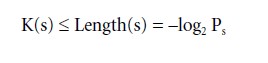
The difference between Length(s) and the length of its shortest description K(s) is the redundancy R in s:

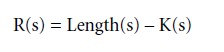
K(s) has been proven not to be obtainable by computational means. Approximating K(s) is not entirely an art, however. Computer programmers use software for optimizing computation, in effect reducing the length of the algorithm they have written – without showing that the result is indeed the shortest possible description. Good computer programmers recognize the difference between the unavoidable complexity K(s) and the dispensable redundancy R(s).

In the evolution of computer languages, compilers have become more powerful, allowing for writing shorter programs, but taking up more computer space and time. This has greatly accelerated information technological developments. There exists a proposal to shift attention from theorizing the shortest programs for solving a problem, to the shortest time required to accomplish the same.

Critiques and Comments

While Shannon’s theory was eagerly embraced by early human communication theorists, its concepts were acquired largely through secondary sources, e.g., Weaver’s interpretation (Shannon & Weaver 1949, 95 –117). Recent communication scholarship has developed doubts about the conceptual significance of information theory. While critical examinations are healthy, they should address the theory itself.

One widespread misconception results from the metaphors of information used in interpretations of the theory. Reference to the communication of information, information content, and signals that carry information all construct information as an entity that one could acquire, possess, or be lacking. Shannon’s writing does not support such concepts. Instead, he wrote of entropies, theorized communication, carefully avoiding issues of meaning, and refusing to name his theory “information theory.”

Another misconception stems from reading a “schematic diagram” (Shannon & Weaver 1949, 5) that Shannon used in his introduction to contextualize his theory, showing unidirectional arrows from a sender through a channel to a receiver, as “the Shannon model of communication” However, this diagram is certainly not a model of his theory. At Bell Laboratories, where Shannon worked, nobody could have failed to see the two-way nature of telephone communication, and Shannon’s concept of a channel is perfectly symmetrical. Critics of linearity have a point, though not the one they are making: Shannon’s calculus, grounded in probability theory, blinded him to circular communication, e.g., from A to B to C to A. However, Klaus Krippendorff (1986, 57ff.) extended Shannon’s theory to include such and more elaborate recursive communication structures.

Other critics impute underlying purposes: the intention of senders to control receivers. However, Shannon’s theory concerns reproducibility in the face of interferences and breakdowns, not control. Reliable communication technology is the foundation of contemporary information society. Its capacity to store, compute, and communicate is measured in bits or bytes and paid for accordingly, and has expanded ever since.

The failure of communication researchers to differentiate engineering and everyday distinctions in human interfaces with communication technologies has created a false barrier against Shannon-type theories. The fact that the number of bits transmitted to television images far exceeds the number of concepts that ordinary viewers have at their disposal to see these images is no justification for privileging the former as objective quantities and dismissing the latter as subjective phenomena. The difference is due to meaningful equivocation, which can be studied.

A more reasonable complaint concerns the conception of uncertainty. Mathematical theories can be quite rigid whereas the uncertainties that people experience are fluid. Nevertheless, human information processing has been examined in communication research, for example, by uncertainty reduction theory, which received its impetus from information theory.

Finally, information theory is not meant to predict behaviors. It theorizes limits to what can be done – just as thermodynamics does. Whereas the logical theory addresses possible distinctions and explores the differences they could make elsewhere the statistical theory concerns capacities of communication media and investigates ways to improve their reliability, and the algorithmic theory concerns computations and examines their efficiencies. Their common unit of measurement concerns essential human activities: distinguishing, conceptualizing, inferring, and deciding among alternatives.

References:

1. Ashby, W. R. (1981). Two tables of identities governing information flows within large systems. In R. Conant (ed.), Mechanisms of intelligence: Ross Ashby’s writings on cybernetics. Seaside, CA: Intersystems, pp. 159 –164.
2. Bar-Hillel, Y. (1964). Language and information. Reading, MA: Addison-Wesley. Bateson, G. (1972). Steps to an ecology of mind. New York: Ballantine Books.
3. Kolmogorov, A. N. (1965). Three approaches to the quantitative definition of information. Problemy Peredachi Informatsii, 1(1), 3 –11.
4. Krippendorff, K. (1967). An examination of content analysis: A proposal for a framework and an information calculus for message analytic situations. PhD dissertation, University of Illinois.
5. Krippendorff, K. (1986). Information theory; Structural models for qualitative data. Beverly Hills, CA: Sage.
6. Shannon, C. E., & Weaver, W. (1949). The mathematical theory of communication. Urbana, IL: University of Illinois Press.

Back to Communication Theory and Philosophy.